An Important Computational Advantage of Structured SDR Coding (e.g., Sparsey) over Flat SDR Coding (e.g. Kanerva) Models and over Optimization-centric "Sparse Coding" (e.g., Olshausen & Field) Models
In SDR, each item (percept, concept) is represented by a small subset of units chosen from a much larger field of units. Figure 1 shows two kinds of SDR coding field, a “flat” field of M binary units, e.g., as used in Kanerva’s "Sparse Disributed Memory" (SDM), and a structured field of units as used in Sparsey, where the field consists Q winner-take-all (WTA) competitive modules (CMs), each with K binary units; here, Q=19, K=10. To make the two fields commensurate, we define M=K×Q. In both cases, 10% (1/10) of the units are active in any code; example codes shown in the figure.
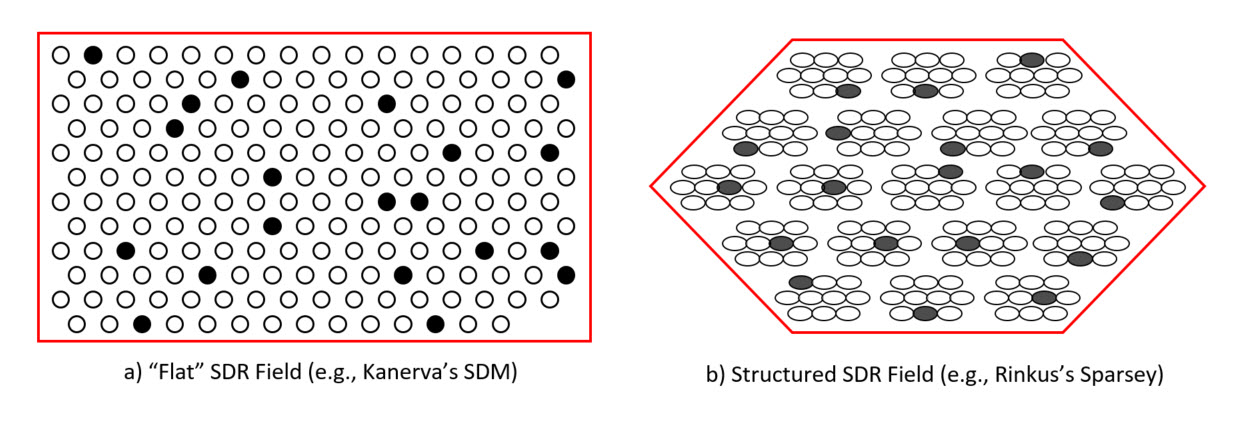
Figure 1: Two kinds of SDR coding fields. a) A “flat”, Kanerva-type SDR field of M=190 units. b) A structured, Sparsey SDR field of Q=19 WTA competitive modules (CMs), each with K=10 units, for a total of K×Q = M units
Sparsey’s structured format has an important computational advantage over the flat field. Consider that in either the flat or structured case, the act of activating a code has two conceptual pieces:
- Selecting the specific units that will be activated; and
- Enforcing that only those selected units activate (i.e., enforcing the sparsity).
In Sparsey’s case, these two pieces are computationally one: no additional computational steps beyond choosing the winner in each CM are needed specifically to enforce sparsity. Thus sparsity is enforced architecturally, or statically. Specifically, a single iteration over a CM’s K units finds the most implicated (e.g., on the basis of the input summations) unit and this is done for each of the Q CMs, i.e., a total of K×Q = M comparisons to determine the whole code. In contrast, the SDM is essentially one big Q-WTA field, i.e., the Q most implicated units out of the entire field are activated. Minimally, this requires iterating over all M units comprising the field to find the max, then iterating over the M-1 remaining units to find the second most implicated unit, etc., Q times, i.e., M + M-1 + … + M-Q comparisons. If Q << M, this is approximately M×Q comparison. Thus, Sparsey’s architectural enforcement of sparsity is a factor Q more efficient than is possible for “flat” field, where, in practical systems, Q will be at least order 100.
In fact, Sparsey enjoys this same advantage (see this post) with respect to any optimization-centric “sparse coding” model in which a sparsity penalty term, i.e., some norm on the total activity of the coding field, is added to the objective function, e.g., Olshausen & Field, and thus adds significant computation. In these types of models the coding field is a flat field of units and the two conceptual pieces of selecting the units to be included in a code (which in such models, is generally an iterative process of convergence, involving many epochs over the whole training set, as opposed to Sparsey’s sing-trial code selection process) and enforcing sparsity are even more explicitly separate computationally than for the Q-WTA SDR coding field.
