Neurithmic Systems's primary goals

  1. Discover the information representation and algorithm(s), e.g., for learning, memory, recognition, inference, recall, used in the brain (neocortex, hippocampus, other regions).  This includes the essential principle that neocortex is a hierarchy of numerous semi-autonomous coding fields, i.e., macrocolumns, which allows explicit representation of the recursive, compositional (part-whole) structure of natural object/events.
  2. Develop extremely efficient, scalable models, based on these representations and algorithms, which do on-line (single/few-trial) learning of spatial and sequential patterns and probabilistic inference/reasoning over the learned patterns, e.g., similarity-based (i.e., approximate nearest-neighbor) retrieval, classification, prediction, e.g., for video event recognition and understanding, as well as for other modalities and multi-modal inputs, e.g., visual + auditory + text.

Our work is founded on the idea that in the brain, especially cortex, information is represented in the form of sparse distributed codes (SDC) [a.k.a., sparse distributed representations (SDR)], a particular instantiation of Hebb's "cell assembly" and "phase sequence" concepts. Our modular SDC (MSDC) format is visible in simulations below, most clearly in each of the coding fields (hexagons) in the third panel of middle video.

Note: SDC is different than (and completely compatible with) "sparse coding" (Olshausen & Field). Sparse coding is fundamentally about the nature of the input space and agnostic as to whether the representation is localist or distributed, whereas SDC is fundamentally about the nature of the representation space.

Highlights

  • Presenting poster "The world model emerges in cortex as the pattern of intersections of sparse distributed codes of individual inputs" at Frontiers in NeuroAI symposium at Harvard's Kempner Institute (June 5-6, 2025) (Poster page)
  • 30-min video describing the hierarchical nature of a Sparsey cortical model.
  • "Semantic memory as a computationally free side-effect of sparse distributed generative episodic memory" GEM 2023 (Talk). (Accepted Abs.)
  • "A Radically New Theory of how the Brain Represents and Computes with Probabilities" Presented at ACAIN 2023. (Paper) (Springer site).
  • "The Classical Tuning Function is an Artifact of a Neuron's Participations in Multiple Cell Assemblies" Sub'd to Conf. on Cognitive Computational Neuroscience 2023. (Abstract)
  • "World Model Formation as a Side-effect of Non-optimization-based Unsupervised Episodic Memory" Accepted as poster, Int'l Conf. on Neuromorphic, Natural and Physical Computing (NNPC) 2023. (Abstract)
  • "A cell assembly simultaneously transmits the full likelihood distribution via an atemporal combinatorial spike code" Accepted as poster, NNPC 2023. (Abstract)
  • "A cell assembly transmits the full likelihood distribution via an atemporal combinatorial spike code". Sub'd to COSYNE 2023. (Abstract)(Rejected, here is the review)
  • "A combinatorial population code can simultaneously transmit the full similarity (likelihood) distribution via an atemporal first-spike code." Accepted poster at NAISys. Nov. 9-12, 2020. (Abstract)
  • Invited Talk: The Coming KB Paradigm Shift: Representing Knowledge with Sparse Embeddings. Presented at “Intelligent Systems with Real-Time Learning, Knowledge Bases and Information Retrieval" Army Science Planning and Strategy Meeting (ASPSM). Hosts: Doug Summers-Stay, Brian Sadler. UT Austin. Feb 15-16, 2019.
  • "A Hebbian cell assembly is formed at full strength on a single trial". (On Medium) Points out a crucial property of Hebbian cell assemblies that is not often discussed but has BIG implications.
  • Submitted abstract (COSYNE 2019) "Cell assemblies encode full likelihood distributions and communicate via atemporal first-spike codes." (Rejected, here is the review)
  • Blog on Sparsey at mind-builder.
  • Accepted abstract to NIPS Continual Learning Wkshp 2018: "Sparsey, a memory-centric model of on-line, fixed-time, unsupervised continual learning." (also available from NIPS site)
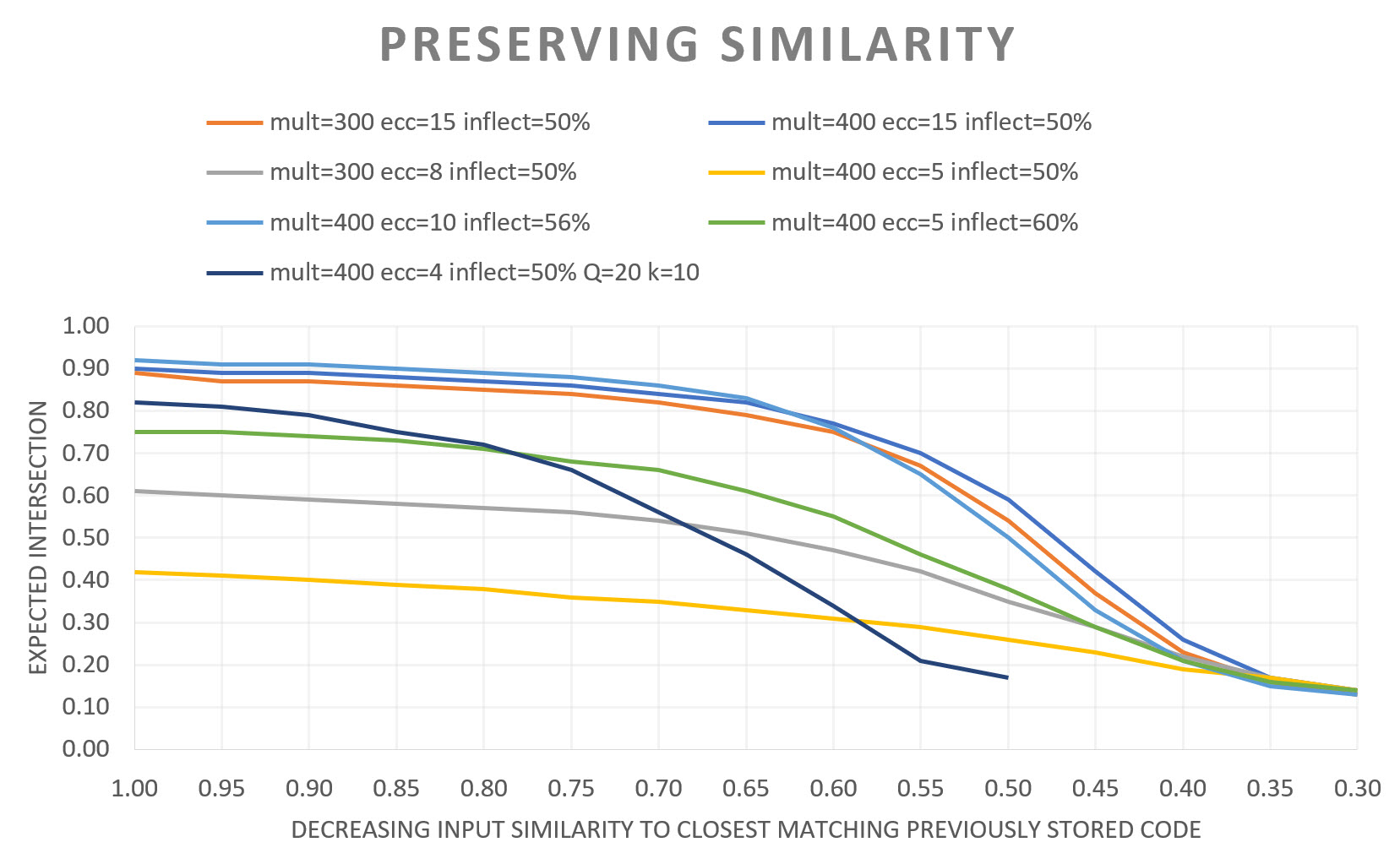
  • JAVA APP showing how Sparsey preserves similarity permitting both learning new items and retrieving the approximate most simlilar item in fixed time. A far simpler and more powerful alternative to locality preserving (and locality sensitive) hashing! Applies equally well to spatial patterns or sequences. Figure below illustrates simlarity preservation (see page).Sparsey preserves similarity from input space to SDR intersection space
  • Accepted (as poster): First Spike Combinatorial Coding: The Key to Brain’s Computational Efficiency. (Abstract) Cognitive Computing 2018
  • 8-18 Talk: Sparse distributed representation, hierarchy, critical periods, metaplasticity: the keys to lifelong fixed-time learning and best-match retrieval. at Biological Distributed Algorithms 2018 (Abstract)
  • Paper: "Superposed Episodic and Semantic Memory via Sparse Distributed Representation" (arxiv)
  • Rod Rinkus Extended Research Statement
  • Sparsey already likely at least as fast without machine parallelism (MP) as gradient-baesd methods are with MP, can easily be sped up by 100-1,000x via simple, existing, non-GPU-based MP, e.g., SIMD, ASIC:
  • Hyper-essay discussing potential weaknesses of Deep Learning models, particularly given Sparsey's unique and powerful properties, including fixed-time, non-optimization-based learning, approximate best-match retrieval, and belief update, of space-time patterns.
  • CCN2017 Submission (Rejected, but I'm sorry, I still think it's great :) The Brain’s Computational Efficiency derives from using Sparse Distributed Representations. Related post on Quora.
  • 4-21-17: Invited Talk: Intel Microarchitecture Technology Lab. Hillsboro, OR (host: Narayan Srinavsa) Sparse Distributed Coding Enables Super-Efficient Probabilistic Modeling.
  • 4-20-17 Invited Talk: IBM Almaden Machine Intelligence Lab. San Jose, CA (host: Winfried Wilcke) Sparse Distributed Coding Enables Super-Efficient Probabilistic Modeling.
  • 3-05-17: NICE 2017 (IBM Almaden) Poster: "A Radically new Theory of How the Brain Represents and Computes with Probabilities"
  • 1-30-17: ArXiv paper describing how Sparsey constitutes a radically different theory [from the mainstream probabilistic population coding (PPC) theories] of how the brain represents and computes with probabilities, which includes radically different concepts / explanations for noise, correlation, and the origin of the classical unimodal single-cell receptive field. An applet explaining core principles in the paper.
  • 8-22-16: Results on MNIST. Preliminary result: 91% on substantial subset of MNIST. To my knowledge, these are the first reported results of ANY SDR-based model (e.g., Numenta, Kanerva, Franklin & Snaider, Hecht-Nielsen) on ANY well-known benchmark! Single-trial learning, no gradients, no MCMC, no need for machine parallelism, just simple Hebbian learning with binary units and effectively binary weights.
  • 3-8-16: Talk at NICE 2016 (Berkeley, March 7-9), focused on the idea that the gains in computational speed possible via algorithmic parallelism (i.e., distributed representations, and specifically, sparse distributed representations, SDR), particularly with regard to probabilistic computing, e.g., belief update, are greater than the gains achievable via machine parallelism.  Though algorithmic and machine parallelism are orthogonal resources and so can be leveraged multiplicatively. (Slides (57meg))
  • 12-15: Historical Highlights for Sparsey: A Talk given at The Redwood Neuroscience Institute in 2004, before it became Numenta. A better 2006 talk (video) at RNI after it moved to Berkeley.
  • 12-15: Preliminary results of hierarchical Sparsey model on Weizmann event recognition benchmark. To our knowledge, these are the first published results for a model based on sparse distributed codes  (SDR) on this or any video event recognition benchmark!
  • 9-15: Brain Works How? ...a new blog with the goal of stimulating discussion of the coming revolution in machine intelligence, sparse distributed representaton.
  • 4-15: Short video explaining hierarchical compositional (part-whole) representation in deep (9-level) Sparsey network.
  • 4-15: Animation showing notional mapping of Sparsey onto Cortex.
  • 4-15: U.S. Patent 8,983,884 B2 awarded (after almost 5 years!) to Gerard Rinkus for "Overcoding and Paring (OP): A Bufferless Chunking Process and Uses Thereof".  A completely novel mechanism for learning / assigning unique "chunk" codes to different sequences that have arbitrarily long prefixes in common, without requiring any buffering of the sequence items.  Interestingly, OP requires the use of sparse distributed representations and is in fact undefined for localist representations.  In addition, it is ideally suited to use in arbitrarily deep hierarchical representations.
  • 3-15: Movie of 8-level Model, with 3,261 macs, in learning/recognition experiment with 64x64 36-frame snippet.  Interestingly, based on a single learning trial, most of the spatiotemporal SDC memory traces are reinstated virtually perfectly even though the "V1" and "V2" traces are only 57% and 85% accurate, respectively.
  • 12-14: Movie of 6-level hexagonal topology Sparsey model recognizing an 8-frame 32x32 natural-derived snippet. Also see below.
  • 12-14: Paper published in Frontiers in Computational Neuroscience: "Sparsey: event recognition via deep hierarchical sparse distributed codes"
  • Neurithmic Systems's YouTube channel
  • 1-15: Fundamentally different concept of a representational (basis) of features in Sparsey compared to that in the localist "sparse basis" (a.k.a. "sparse coding") concept. (PPT slide).
  • CNS 2013 Poster: "A cortical theory of super-efficient probabilistic inference based on sparse distributed representations" (abstract, summary)
  • 2-13: NICE (Neuro-Inspired Computational Elements) Workshop talk (click on "Day1: Session 2" link on NICE page), "Constant-Time Probabilistic Learning & Inference in Hierarchical Sparse Distributed Representations" (PPT)

How Sparsey maps similar inputs to similar codes

The video below (explained in more detail here) illustrates the novel principles by which Sparsey's code selection algorithm (CSA), originally described in 1996 thesis [improved/extended in Rinkus (2010), Rinkus (2014), Rinkus (2017)], causes similar inputs to be mapped to similar codes (SISC). The essential idea is that if inputs (items) are represented by binary MSDCs (codes) of fixed size, Q, where one unit is chosen in each of Q WTA competitive modules (CMs), then we can make the expected intersection sizes of the code, φ(X), of a new item, X, with the codes, φ(Y), of ALL previously stored items, Y, approximately correlate with the similarities of X with each of those stored items by adding noise, of power proportional to the novelty of X (i.e., inversely proportional to the familiarity, G, of X), into the choice processes occurring in each of the Q CMs. It turns out that there is an extremely simple way to compute G(X), i.e., G is simply the average of the max normalized input summations to the Q CMs (as described in the cited papers and here). This addition of noise to the process of choosing a winner in a CM is realized by mapping the (deterministic) normalized input summations, V(i), of each of the CM's K units, i, into a final probability, ρ(i), of winning, through a sigmoid nonlinearity (upper left quandrant of app's GUI) whose shape depends on G. [Actually V is first mapped to an unnormalized (relative) prob, μ, via the nonlinearity, which is then renormalized to the total probability, ρ).]

In particular, if G=1, which implies that the current input, X, is completely familiar (assuming not too many codes have been stored and thus that crosstalk interference is low), i.e., that X was presented in the past and a code for X, φ(X), was chosen and stored at that time, then the sigmoid parameters, e.g., the horizontal position of the inflection point and its eccentricity, are adjusted to greatly increase the win probability of units with high V values relative to units with low V values. Such a condition is depicted around time 1:15 of the video: the eccentricity parameter is increased causing low V values to get squashed towards zero and V values higher than ~0.7 to get pushed toward the max μ (thus, max ρ) value, as can be seen in comparing the V distributions to the ρ distributions at the right of the video. This corresponds to adding very little noise to the winner choice process. That is, the V values, i.e., the input summations, correspond to the "signal". That's because those summations reflect signals arriving from currently active units via synapses whose weights reflect prior learning. Thus, the unit with the max V value in each CM should be chosen winner: that corresponds to perfect reactivation of φ(X), i.e., perfect retrieval X, i.e., perfect transmission of the signal.

At the other end of the spectrum, when G=0, which implies that the current input, X, is completely unfamiliar (completely novel), then the sigmoid is collapsed to the constant (completely flat) function, which maps all V values to the same μ (thus, ρ) value, making all units in a CM equally likely to be chosen winner. This condition is not depicted in the video. For example, it can be achieved simply by setting the range (height) of the sigmoid to zero. In any case, this corresponds to adding maximal noise to the signal, in fact, to bringing the signal-to-power ratio to 0. But this is the most sensible policy for a distributed coding model. That is, when an input X is completely unfamiliar, i.e., unlike any previous input that has been stored, it should be assigned to a new code, φ(X), that is, on average, as far as possible (in terms of Hamming distance) from every previously stored code. This minimizes crosstalk interference and thus, maximizes storage capacity. Choosing winners from the uniform distribution in each CM, i.e., choosing overall codes completely randomly, achieves this.

And, most importantly, as we consider values of G, from 1 to 0, the sigmoid parameters are adjusted so as to gradually increase the noise power relative to signal. In other words, the poilicy is to add noise directly proportional to novelty (or, inversely proportional to familiarity). This results in causing the expected size of intersection of the code, φ(Y), assigned to each new input, Y, to vary directly with the familiarity of X, i.e., with G. That is, this policy of adding noise proportional to novelty into the code selection process statistically preserves similarity, i.e., the SISC property mentioned above. Crucially, the algorithm which achieves this, the CSA, does so with a constant number of computational steps. That is, as each additional input is stored the number of computational steps needed to do that storing remains constant! At the time of this writing (10/04/2024), I know of no other algorithm that achieves this capability. In particular, no locality preserving hashing (LPH) or locality sensitive hashing (LSH) algorithm runs in "fixed time".

The app allows the user to vary three sigmoid parameters, eccentricity, output range, and horizontal position of the inflection point, to see how they affect the noise, and ultimately the statistics of the SISC property.

High-level concepts are hierarchical, compositional, spatiotemporal memory traces

A hierarchical memory trace (engram)—in the form of a Hebbian phase sequence involving hundreds of cell assembly activations across two internal levels (analogs of V1 and V2)—of a visual sequence of a human bending action. Left panel shows binary pixels possibly analogous to very simplified LGN input to cortex. Next panel shows plan of array of V1 macrocolumns ("macs"), specifically, abstract versions of their L2/3 pyramidal pools, receiving input from LGN. Next panel shows array of V2 macs receiving input from the V1 macs. Last panel shows corresponding 3D view and showing some of the bottom-up (U, blue) and horizontal (H, green) connections that would be active in mediating this overall memory trace.   The cyan patch on the input surface shows the union of the receptive fields (RFs) of the active V2 macs.  We son't show the V1 mac RFs, but they are much smaller, e.g., 40-50 pixels.  In general, the RFs of neaby macs overlap (see Figs. 2 and 3 here).  Go Fullscreen to see detail. Or, see this page for more detailed discussion.

Sparse Distributed Coding (SDC) enables a revolution in probabilistic computing

SDC provides massive algorithmic speedup for both learning and approximate best-match retrieval of spatial or spatiotemporal patterns. In fact, Sparsey (formerly, TEMECOR), invented by Dr. Gerard Rinkus in the early 90's, both stores (learns) and retrieves the approximate best-matching stored sequence in fixed time for the life of the system. This was demonstrated in Dr. Rinkus's 1996 Thesis and described in his 2004 and 2006 talks at the Redwood Neuroscience Institute, amongst other places. To date, no other published information processing method achieves this level of performance! Sparsey, implements what computational scientists have long been seeking: computing directly with probability distributions, and moreover, updating from one probability distribution to the next in fixed time, i.e., time that does not increase as the number of hypotheses stored in (represented by) the distribution increases.

The magic of SDC is precisely this: any single active SDC code simultaneously functions not only as the single item (i.e., feature, concept, event) that it represents exactly, but also as the complete probability distribution over all items stored in the database (e.g., discussed here and here). With respect to the model animation shown here, each macrocolumn constitutes an independent database (memory). Because SDCs are fundamentally distributed entities, i.e., in our case, sets of co-active binary units chosen from some much larger pool (e.g., the pool of L2/3 pyramidals of a cortical macrocolumn), whenever one specific SDC code is active, all other stored SDCs are also partially physically active in proportion to how many units they share with the fully active SDC. And, because these shared units are physically active (in neural terms, spiking), all these partially active codes also influence the next state of the computation in downstream fields as well as in the source (field via recurrent pathways). But, the next state of the computation will just be another of the stored SDCs [or, if learning is allowed, a possibly new code that may contain portions (subsets) of previously stored SDCs] that becomes active, which will in general have some other pattern of overlaps with all of the stored SDCs, and thus embody some other probability distribution over the items.

Virtually all graphical probabilistic models to date, e.g., dynamic Bayes nets, HMMs, use localist representations. In addition, influential cortically-inspired recognition models such as Neocognitron and HMAX also use localist representations. This page shows what an SDC-based model of the cortical visual hierarchy would look like. Also see the NICE Workshop and CNS 2013 links at left.

Memory trace of 8-frame 32x32 natural event snippet playing out in a 6-level Sparsey model with 108 macs (proposed analogs of cortical macrocolumns).

This movie shows a memory trace that occurs during an event recognition test trial, when this 6-level model (with 108 macs) is presented with an identical instance to one of the the 30 training snippets. A small fraction of the U, H, and D signals underlying the trace is shown. See this page for more details. What's really happening here is that the Code Selection Algorithm (CSA) [See Rinkus (2014) for description] runs in every mac [having sufficient bottom-up (U) input to be activated] at every level and on every frame. The CSA combines the U, H, and D signals arriving at the mac, computes the overall spatiotemporal familarity of the spatiotemporal moment represented by that total input, and in so doing effectively retrieves (activates the SDR code of) the spatiotemporally closest-matching stored moment in the mac.

eXTReMe Tracker